坐标反算是指依据直线的起点和结尾的坐标,核算直线的水平间隔和坐标方位角的过程。坐标反算一般首要应用于测绘工程、建设工程之中,具体在建筑设计,工程丈量,测绘制图等范畴。总的来说坐标核算分为坐标正算和坐标反算两种,这两种在实践中是较常见的。
定义
坐标反算
依据已知直线的起点和结尾坐标,来核算直线的水平间隔和坐标方位角的过程叫坐标反算。
坐标正算
依据直线的起点坐标、直线的水平间隔以及坐标方位角来核算结尾的坐标的过程叫坐标正算。
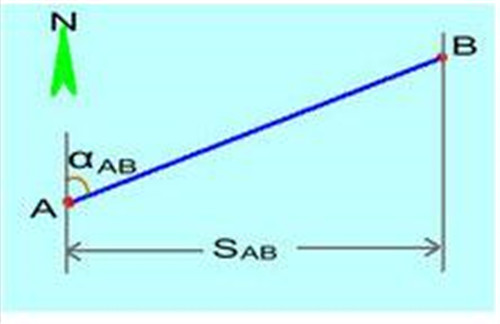
如图中所示,已知一条直线的起点和结尾坐标分别为A点坐标(XA,YA),B点坐标(XB,YB),A点到B点间隔L,A点到B点方位角aAB,经过坐标反算来核算直线AB的水平间隔S ab和坐标方位角α ab。
坐标正算公式: XB=XA+LcosaAB
YB=YA+LsinaAB
坐标反算公式:L^2= (XB-XA)^2+(YB-YA)^2
由于反三角函数核算的结果有多值性
所以在核算坐标方位角α ab之前,要先核算象限角R ab。
核算步骤
①tan R ab=/△y ab/╱/△x ab/=/y b-y a/╱/x b-x a/;
②R ab=arctan/y b-y a/╱/x b-x a/;
③L=/△y ab/╱sinα ab=/△x ab/╱cosα ab。Sab=△y ab。L是A、B两点间间隔,Sab是水平间隔。
④依据“②”中所求的R ab,求坐标方位角α ab,
⑴若坐标方位角为榜首象限角,则:R ab=α ab;
⑵若坐标方位角为第二象限角,则:α ab=180°-R ab;
⑶若坐标方位角为第三象限角,则:α ab=180°+R ab;
⑷若坐标方位角为第四象限角,则:α ab=360°-R ab。
附注
坐标方位角:直线的方向是用方位角来表明的,其间以坐标北方向为基准方向,顺时针旋转到直线的水平视点,称为该直线的坐标方位角。
象限角划分:榜首象限角:0°~90°
第二象限角:90°~180°
第三象限角:180°~270°
第四象限角:270°~360°
另留意:此象限角的划分与数学中的象限角不同,应留意!
现场确认坐标系
假如找到两个基准点A(N3000,E4500,Z100),B(N2900,E5500,Z120),则能够依据基准点坐标值反推坐标系,找到N,E方向。
首先确认N,E方向:
从E坐标能够发现,B点E坐标大于A点,所以B点应在A点的东面。再看B的N坐标小于A点,故B点应在A点南面。即B点在A点东南面。
求出直线AB与E坐标的夹角:
a=atg((Nb-Na)/(Eb-Ea))
-90degree<=a<=90degree
若a>0,则直线从A到B成右上方向走向。若a<0,则直线从A向B成左下方向走向。若a=0,则AB平行于E轴线。若a=+90或-90度,则直线垂直于E轴线。由此能够确认现场的NE坐标系。
坐标反算计算原理与步骤简介图2